How to Draw a Machete

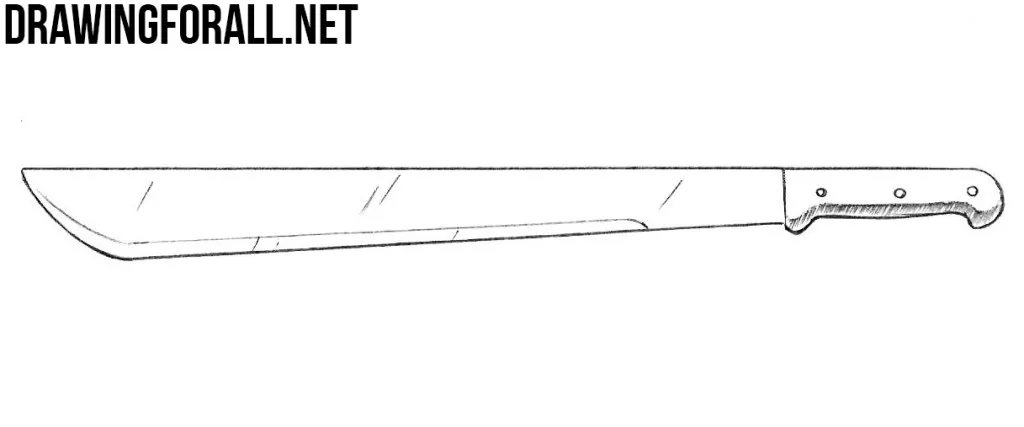
Kind time of the day, dear artists. In this drawing lesson we’ll show you how to draw a machete. This drawing lesson is a part of the drawing lessons about cold weapons, such as sword and katana.

 

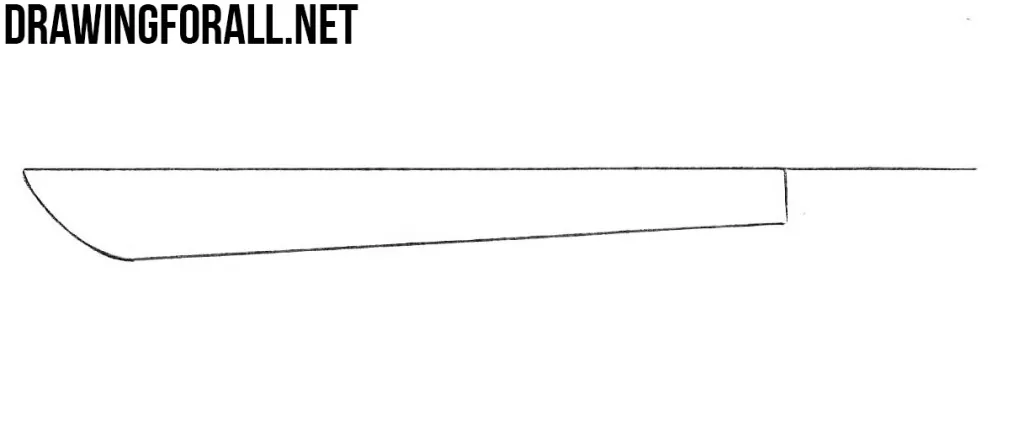
Step 1

First of all draw a long horizontal line. This will be the upper edge of our machete.

Step 2

Now draw another line under the line from the previous step, as in our example.

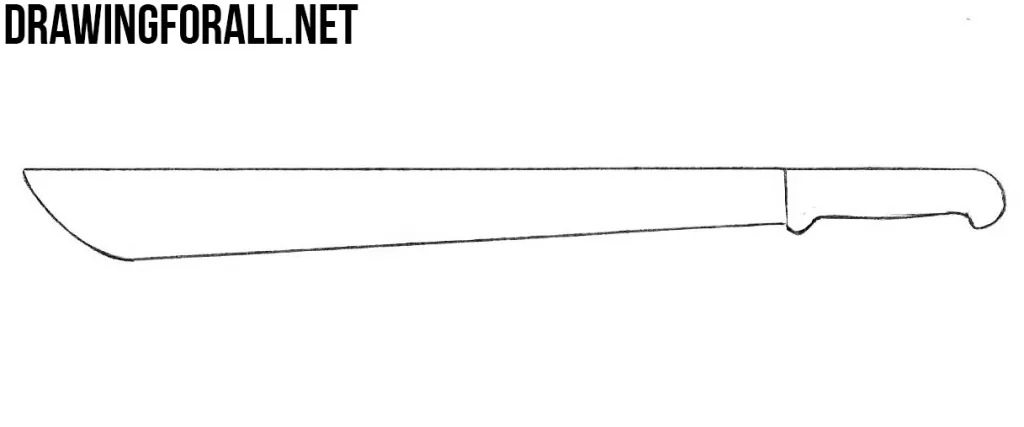
Step 3

Using the curved line draw the grip of our machete.

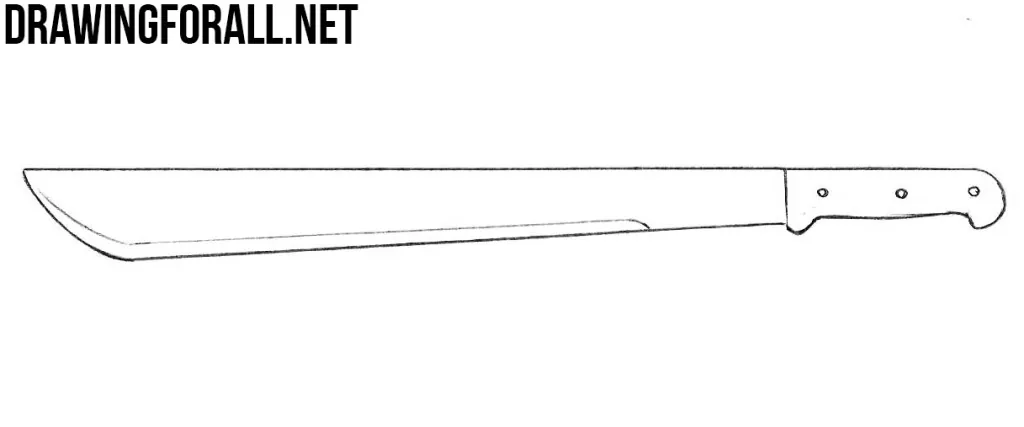
Step 4

Draw a line of sharpening on the blade and three rivets on the grip.

Step 5

Now using short strokes add glare on the blade and shadows on the grip.

 

It was a drawing lesson about how to draw a machete step by step. Do not forget to subscribe to us on social networks, share this drawing lesson with your friends and write your wishes in the commentary to this article.